Distribución normal

La distribución normal consiste en la representación gráfica de una realidad estadística.

Se fundamenta en los estudios del físico y matemático Carl Friedrich Gauss que, en el Siglo XIX, publicó sus estudios sobre la función gaussiana, función matemática que encuentra la probabilidad en una variable continua y que se representa mediante la campana de Gauss.

La idea es conocer, en un estudio estadístico, como se distribuye la población estudiada según una determinada característica; y hablamos de función normal porque, con muestras suficientemente representativas, los resultados obtenidos serán siempre los mismo que serán los resultados de la población general, es decir, si hacemos varias encuestas diferentes las distribuciones no cambiarán y serán iguales.

Vamos a explicarlo con un ejemplo: escogemos a un grupo de personas y el dato que nos interesa que, por ejemplo, es su edad: con el número de personas que tienen cada edad representamos la distribución mediante un eje de coordenadas, en el eje x las edades y en el eje y el número de personas que tienen esas edades de la siguiente manera:

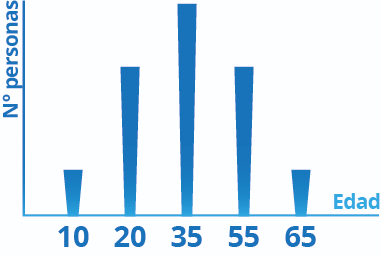
En este ejemplo, de las personas estudiadas, hay muchísimas que tienen 35 años, muchas que tienen 55 y muchas 20, ya hay menos que tengan 65 y también menos que tengan 10 años.

Con este gráfico creamos una curva de distribución normal, que sería:

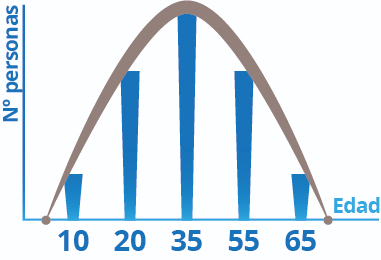
En ella el valor medio es, por un lado, el valor que se nos dá de manera más abundante (en este ejemplo los 35 años) y es, también, la media de la población, es la moda.

La media de la población se representa con la letra griega mu (μ).

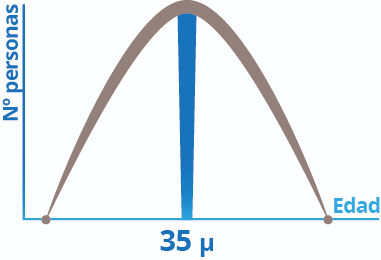
La curva es perfectamente simétrica en sus dos lados, esto significa que la distribución de edades es totalmente equivalente para los que son mayores de 35 y los menores.

Ésto que hemos hecho con las edades de los sujetos que forman la muestra y, por tanto, de la población estudiada, se puede hacer con muchísimas otras características que queramos estudiar: el nivel de ingresos, de gastos en determinados bienes, la altura, el peso, etc.

La desviación típica, que se representa con la letra griega sigma (σ) nos dice hasta qué punto los que no pertenecen a la media  están lejos o cerca de ella, es decir, si es una población muy homogénea y están los sujetos muy cercanos a la media o si es heterogénea y están muy alejados.

Si la situación es homogénea la desviación σ es muy reducida y los sujetos están todos en niveles muy próximos a la media μ y la curva será muy afilada.

Si la situación es muy heterogénea decimos que la desviación σ es muy elevada y la curva será mucho más plana: esto significa que encontramos muestras de todos los tipos en cantidades muy apreciables con resultados muy alejados de la media por un lado y por otro.